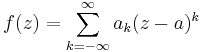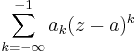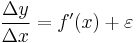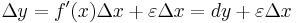Principal part

In mathematics, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series of a function.

Contents

Laurent series definition

The principal part at 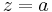z=a of a function

f(z) = \sum_{k=-\infty}^\infty a_k (z-a)^k

is the portion of the Laurent series consisting of terms with negative degree. That is,

\sum_{k=-\infty}^{-1} a_k (z-a)^k

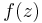is the principal part of f at a . f(z) has an essential singularity at a, if and only if the principal part is an infinite sum.

Other definitions

Calculus

Consider the difference between the function differential and the actual increment:

\frac{\Delta y}{\Delta x}=f'(x)%2B\varepsilon
\Delta y=f'(x)\Delta x %2B\varepsilon \Delta x = dy%2B\varepsilon \Delta x

The differential dy is sometimes called the principal (linear) part of the function increment Δy.

Distribution theory

The term principal part is also used for certain kinds of distributions having a singular support at a single point.

See also

External links